6. Model validation and uncertainty

6.1. Uncertainty

6.1.1. Simulation uncertainty

The main purpose of the model is to assess the impact of an intervention, or alternative scenarios. In order to do this, the model is run twice and outcomes are compared (e.g. obesity vs. no obesity).

To estimate simulation uncertainty, the simulation is distributed into subsamples which allows us to compute the mean and standard deviation of all outcomes.

6.1.2. Baseline uncertainty

For baseline projections, one source of uncertainty is the input parameters used. Due to computing time constraints, this uncertainty is not included in the model. Instead the model is run with mid-parameter estimates. The underlying approach to this assumption is that most of the uncertainty at baseline ‘disappears’ when computing differences in impact. Therefore, the difference between mean and standard deviation represents the true uncertainty across scenarios.

6.1.3. Intervention uncertainty

The majority of intervention uncertainty comes from uncertainty surrounding the intervention’s parameters. The model can estimate this uncertainty by running the intervention with different sets of parameters which provide different estimate outcomes.

6.2. Validation Results

6.2.1. Demography

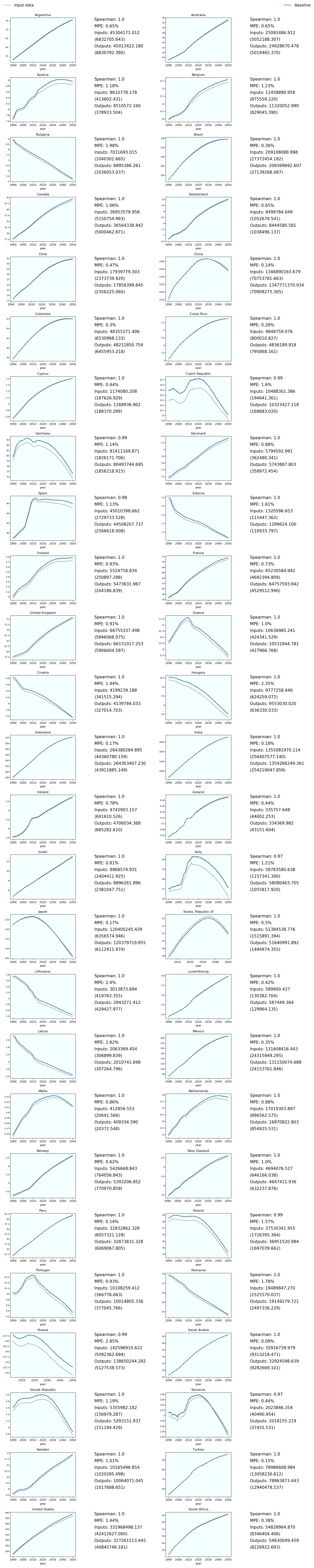
../_images/population_yearly_0.png

Fig. 6.1 Total Population, input and simulated output

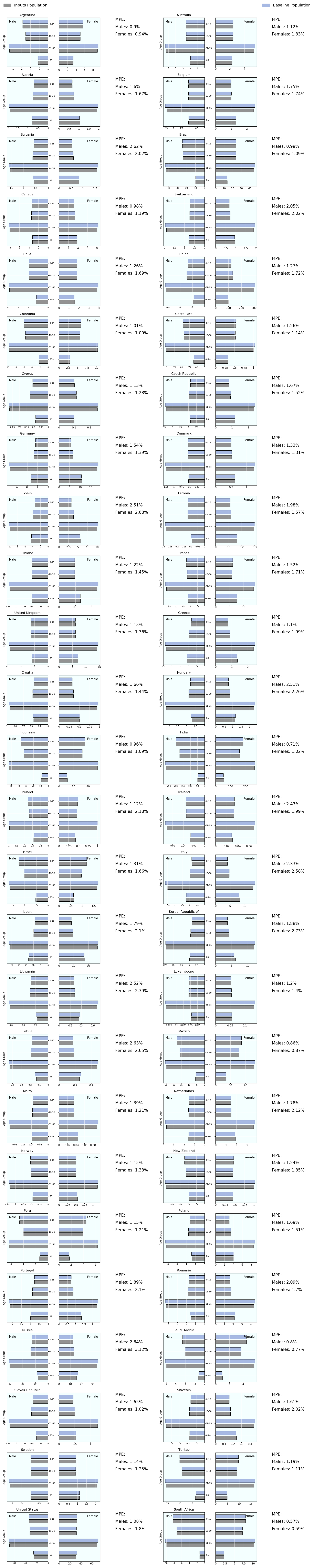
../_images/population_AG_0.png

Fig. 6.2 Population by age-group (averages over 2005-2015), input and simulated output

6.2.2. Risk Factors

6.2.2.1. BMI

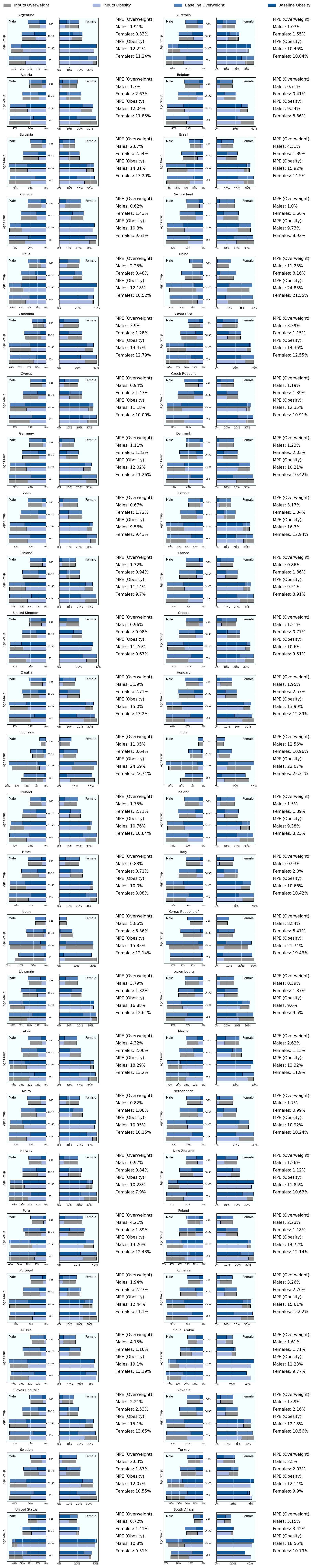
../_images/BMI_0.png

Fig. 6.3 Overweight and obesity prevalence by age-group (averages over 2005-2015), input and simulated output

6.2.3. Diseases

6.2.3.1. Diabetes

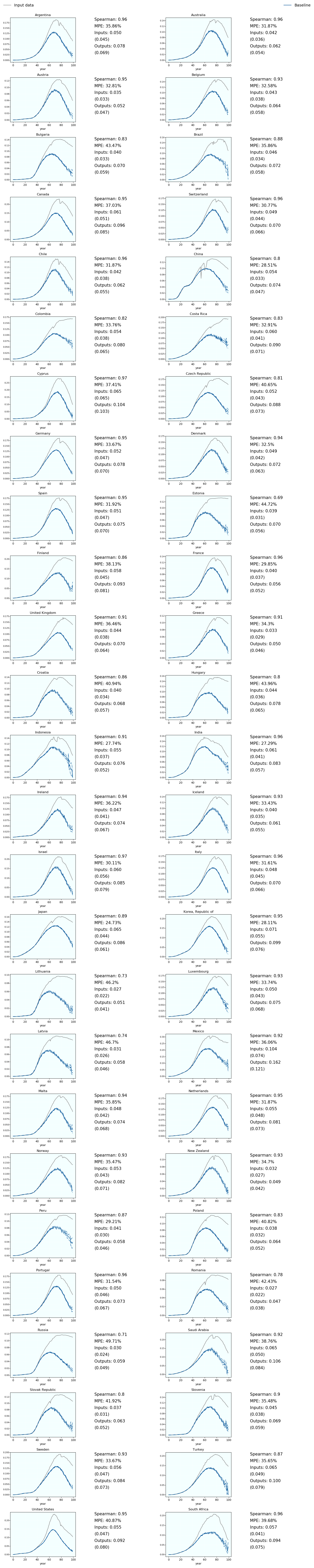
../_images/Diabetes_M_0.png

Fig. 6.4 2015 Diabetes prevalence for men (input and simulated output)

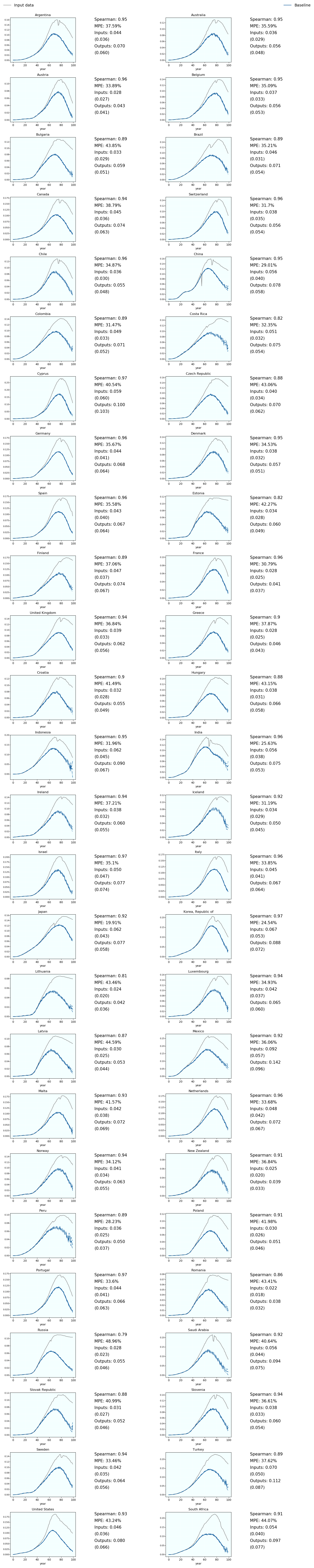
../_images/Diabetes_f_0.png

Fig. 6.5 2015 Diabetes prevalence for women (input and simulated output)

6.2.3.2. Cancers

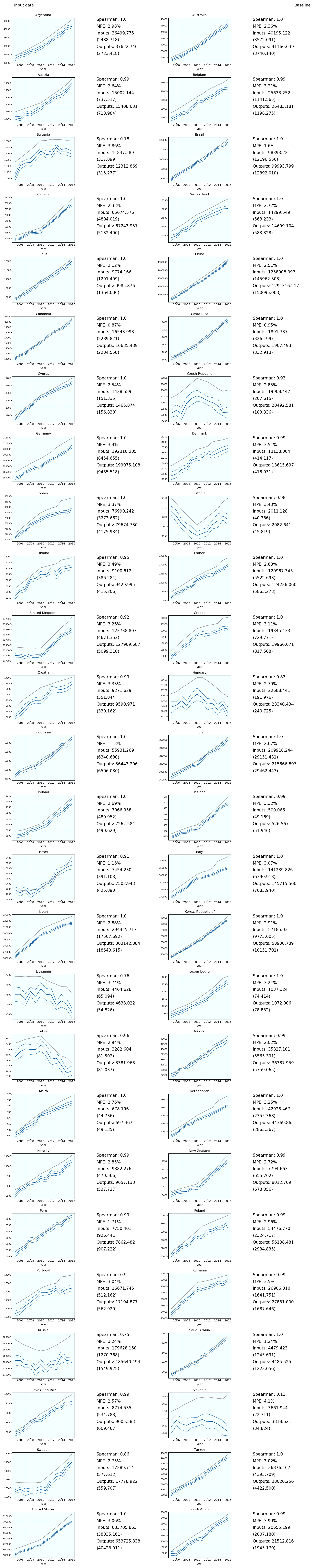
../_images/cancer_incidence_0.png

Fig. 6.6 Cancer incidence cases (averages over 2005_2015) inputs and outputs